OpenGL Camera default

- OpenGL의 카메라의 Default는 원점(origin)에 위치하고 -z방향을 바라봄
Camera Motion
1. Camera coordinate system
Figure1에서 본 좌표와 같이 OpenGL의 coordinate system은 right-handed system으로 되어있다.
이와 달리 view (camera, eye) coordinate system은 어떻게 되어있을까

아래와 같이 설정
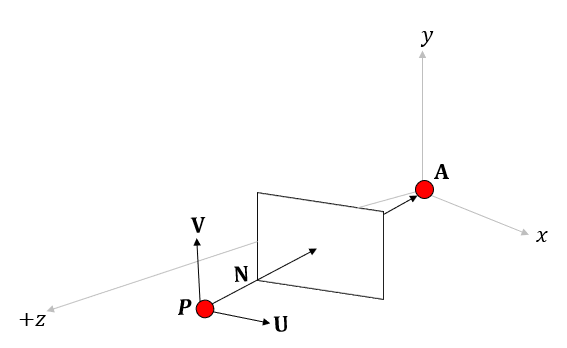
- P : camera postion (COP)
- A : 카메라가 바라보고 있는 target position ( = at point )
- V : up vector, 카메라의 머리 위쪽 방향을 나타내는 vector ( y direction in camera coordinates )
- U : 카메라의 오른쪽 방향의 vector ( x direction in camera coordinates )
- N : COP로 부터 target position 방향의 vector, view plane의 normal vector
\( \rightarrow \) +N방향은 우리 쪽으로 부터 화면 안쪽 방향을 향하고 있다 (world space와 반대)
그렇다면, N, U, V 는 어떻게 구할까. 먼저, 가상의 up vector v'을 설정한다 v'은 많은 경우 world space의 y축인 (0,1,0)으로 설정한다(정확한 V방향은 아니며 UVN을 구하기 위한 parameter이다).

- N = Norm(n), n = A-P
- U = Norm(u), u = n x v'
- V = Norm(v), v = u x n
* Transformation : World space -> Camera space
U, V, N, P 모두 world space를 기준으로 표현한 것으로 이를 통해 쉽게 camera space에서 world space로 transformation하는 matrix를 구할 수 있다 - 참조 (2022.04.01 - [Graphics] - Homogeneous Coordinates (동차좌표))

위의 matrix는 camera space -> world space이므로 이 matrix를 inverse한 matrix가 World space 에서 Camera space로 transformation하는 matrix가 된다(아래의 matrix).

* Example
World coordinates system에 Camera parameter P = (1, -1, 5), A = (0, 0, 0), v' = (0,1,0)이 존재할때
- n = A - P = (-1, 1, -5) -> N = ()
- u = n x v' = (5, 0, -1) -> U = ( \( \frac{5}{\sqrt{26}}, 0, -\frac{1}{\sqrt{26}} \) )
- v = u x n = (1, 26, 5) -> V = ( \( \frac{1}{3\sqrt{78}}, \frac{\sqrt{\frac{26}{3}}}{3}, \frac{5}{3\sqrt{78}} \) )
* glm::lookAt


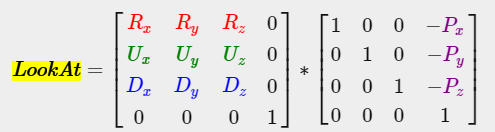
glm::lookAt은 COP와 target, virtual vector가 주어지면 world에서 view space로 변환하는 matrix를 구할 수 있다.
'Graphics' 카테고리의 다른 글
| Viewing & Camera -1 이론 (0) | 2022.04.06 |
|---|---|
| Transformation in homogeneous coordinates (0) | 2022.04.02 |
| Homogeneous Coordinates (동차좌표) (0) | 2022.04.01 |
| OpenGL? (0) | 2022.02.28 |
| API ? (0) | 2022.02.28 |




댓글